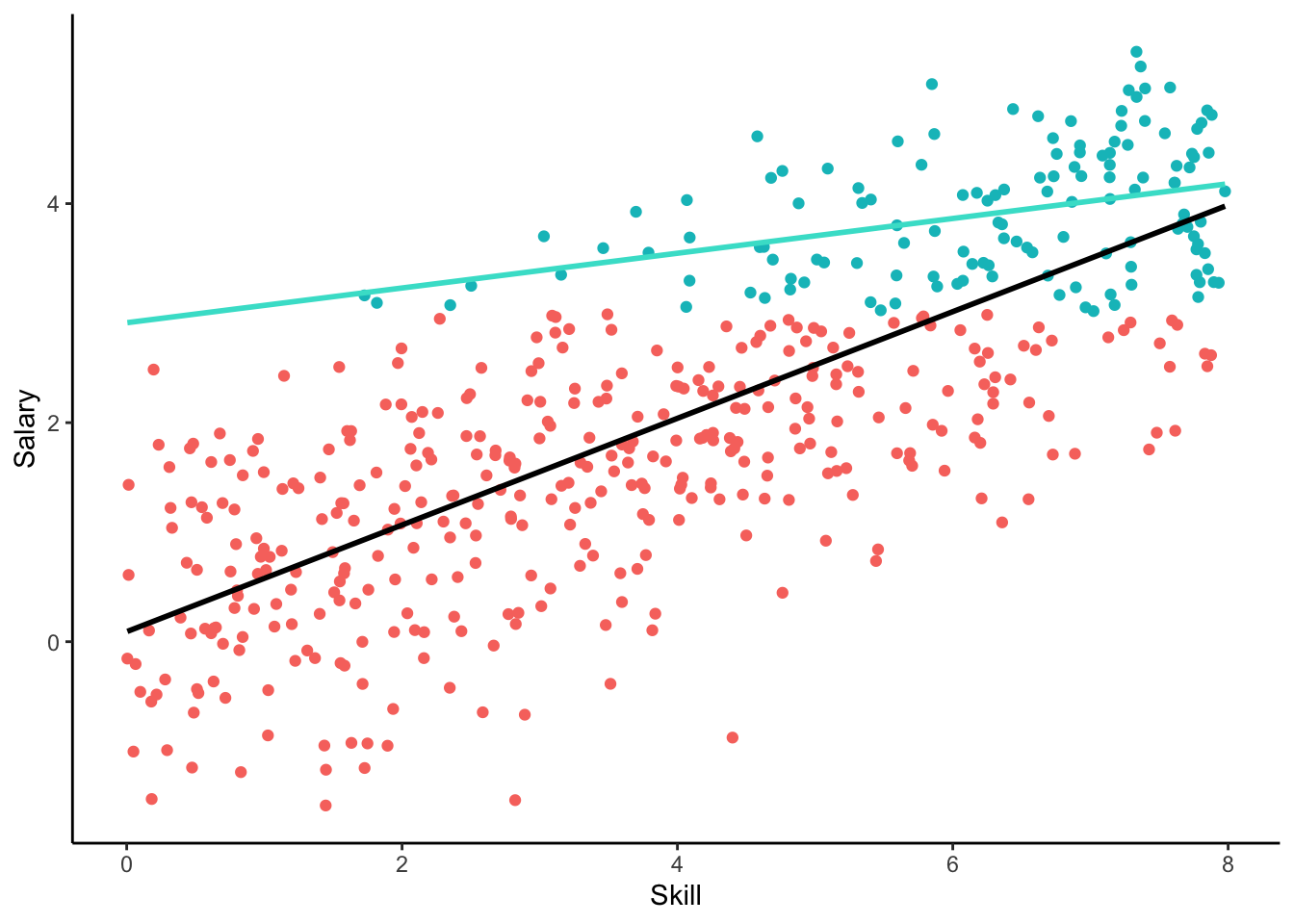
Selection effects

A simple simulation study

Let’s imagine a profession where your salary is linearly related to your skill level:

\[ \texttt{salary}_i = \alpha + \beta\;\texttt{skill}_i + \varepsilon_i, \qquad \varepsilon_i \overset{iid}{\sim} \operatorname{N}(0, \sigma^2)\;. \]

Given a random sample we can easily get an unbiased estimate of \(\beta\), but in applied work the mechanisms determining the sample are not fully random. For example, imagine that we live in a world with universal basic income where only people with a salary above a certain threshold are willing to work. What will happen with our estimate of \(\beta\) when we subset our data to only include people with a salary above the threshold?

To explore this we generate a data set of \(500\) observation, where the values of \(\texttt{skill}\) are random draws from a \(U(0, 8)\) distribution, with \(\alpha = 0\) and \(\beta = 1/2\). The cutoff for \(\texttt{salary}\), i.e. the level of universal basic income, is set to \(3\).

Figure 1: Estimated regression lines based on the full sample (black), and a subset consisting of only those who work (turquoise).

As can be seen in Figure 1, limiting our sample to the subset of people who actually work biases our estimate of \(\beta\), in this case leading to a sever underestimate. This is what is known as a selection effect. Interesting enough, subsetting based on the variable skill would not have biased our estimate of \(\beta\).

The reason for the bias is that in the model that we estimate with only the working subsample, \(\texttt{skill}\) is no longer exogenous. The assumption of exogeneity states that the conditional expectation of the errors given the covariate should be \(0\) \({(\operatorname{E}(\varepsilon \mid \texttt{skill}) = 0)}\) which does not hold in the subsample. For example, when \(\texttt{skill} = 6\) the errors follow a normal distribution truncated at zero resulting in all nonnegative errors.

All is not lost however, and as long as we can model the selection mechanism we can remove the bias in our estimates. To do this, we break our model down into two equations. The first equation we will call the selection equation. It models the conditional probability that a person works, given their skill level. The second equation we will call the outcome equation. It models the conditional expectation of the wage, given the skill level. Our main interest lies in estimating the \(\beta\) coefficient in the outcome regression, given that we only observe the outcome for those who work. We will use the selection equation as a first step, which will help us correct for this bias. This method is known as Heckman correction (Heckman 1979).

References

Heckman, James J. 1979. “Sample Selection Bias as a Specification Error.” Econometrica 47 (1): 153. https://doi.org/10.2307/1912352.